- 帖子
前两天推敲西方伪作“斐波那契《计算之书》(Fibonacci's Liber Abaci）”，发现该书中抄录许多和中国古代算书中雷同的算术题，其中第 12 章有一题：
“七个老人去罗马。他们中每个人有 7 个骡子， 每个骡子背了 7 个袋子， 每个袋子中有 7 片面包， 每片面包有7 把小刀 ，每把小刀有 7 个鞘。求上述和 。”
再看我们的《孙子算经》卷下有题：
题：“今有出门望见九堤，堤有九木，木有九枝，枝有九巢，巢有九禽，禽有九雏，雏有九毛，毛有九色。问：各几何？
答：答曰：木八十一枝，七百二十九巢，六千五百六十一禽，五万九千四十九雏，五十三万一千四百四十一毛，四百七十八万二千九百六十九色，四千三 百四万六千七百二十一。”
术：“术曰：置九堤以九乘之，得木之数；又以九乘之，得枝之数；又以九乘之，得巢之数 ；又以九乘之，得禽之数；又以九乘之，得雏之数；又以九乘之，得毛之数；又以九乘之 ，得色之数。”（注：“术”即今日所说的“算法”。）
两厢比较，不得不说，他们的题抄的如此拙劣：骡子 → 袋子 → 面包 → 刀子 → 刀鞘。物品递进关系没有必然的联系，即使有，也不符合常识，别扭。
再看我们的算经：九堤 → 堤有九木 → 木有九枝 → 枝有九巢 → 巢有九禽 → 禽有九雏 → 雏有九毛 → 毛有九色。层层递进，越来越小，越来越细，但是其中各事物的关系又非常契合自然的韵律和道理，自然界中这些事物的关系就应该如此。这么好的题，完全可以做小学语文教材了。
又见《张丘建算经》中的最后一问，就是闻名于世的 “百鸡问题”，这是一个不定方程问题，书中给出了三组解，其解法仅给 15 字：
题：“今有鸡翁一，直钱五；鸡母一，直钱三；鸡雏三，直钱一；凡百钱买鸡百只，问鸡翁、母、雏各几何？”
答：“答曰：鸡翁四，直钱二十；鸡母十八，直钱五十四；鸡雏七十八，直钱二十六。
又答：鸡翁八，直钱四十；鸡母十一，直钱三十三；鸡雏八十一，直钱二十七。
又答：鸡翁十二，直钱六十；鸡母四，直钱十二；鸡雏八十四，直钱二十八。”
术：“术曰：鸡翁每增四，鸡母每减七，鸡雏每益三，即得。”
鸡翁，鸡母，鸡雏。这三者之间的关系多么融洽和谐，我们小时候也养过鸡啊，实在是太亲切了。
再看 “斐波那契《计算之书》(Fibonacci's Liber Abaci）”抄的题，《计算之书》11 章：
“有人买鸟。斑鸠1只3钱币，鸽子1只2钱币，2只麻雀1钱币。30 个钱币买30只鸟。我们需要知道各种鸟他买了多少 ? ”
斑鸠，鸽子，麻雀。对，三种都算鸟，也许斑鸠属禽类？然而他们之间没有什么必然的相互之间的联系。所以这道题相比《张丘建算经》中的题就显得不自然，生硬。这是抄写的人即要保留原题，又需要更改一些地方，使得抄的题与原题看上去不一样，这就是痕迹。
有道理
计算之书是以歌谣形式记载这些东西的 有些就是为了押韵 再说文化不同 这么评判着实太偏颇
@正音悉达 #17157
有人说中国古代就没有数学，除了勾股定理外什么也没有。同时对欧洲中世纪吹的天花乱坠，比如伟大的笛卡尔，斐波那契数列等。
------对这话你也会说“这么评判着实太偏颇”吗？
但按照经验，你会突然保持沉默
@正音悉达 #17157
你告诉我这是歌谣？押韵？你欺负我不懂拉丁文？还是欺负我不懂英文？还是我智商欠费，分不清正儿八经书籍和歌谣的区别？你告诉我一本算书竟然可以完全用歌谣记录？哦，忘了，瞎眼古希腊人荷马还能逆天地创作两部长篇史诗传颂至今呢，都是奇才，何况区区一步算书呢？是吧！
@gsyrzjy #17163
这是面对其他的文化如何自处的问题
我们说“堤有九木，木有九枝” 觉得这个很有逻辑性 很有美感 这个当然是根植于我们所受到的文化熏陶的结果
“骡子 → 袋子 → 面包”这样的描述真的“生硬别扭” 真的是对孙子算经的“拙劣地抄题”吗？
至于“有人说中国古代就没有数学，除了勾股定理外什么也没有。同时对欧洲中世纪吹的天花乱坠，比如伟大的笛卡尔，斐波那契数列等。”
这句话当然要先问是不是，再去评价。
当然，经过多方面枚举后，往往却是得出来的结果是，中国古代数学理论上的建树不如国外。但是我想反问，凭什么中国古代所有的方面，都要领先于其他国家？凭什么世界的文化分为了两个部分，一个是“中国”，一个是“西方”；仅凭中国一国之力，为什么要与其他的所有国家进行功利性质地比较？
中国是一个具有悠久文明的古国，历史上凝结了丰富多彩的文化宝藏，这一点当然足够我们自豪。但是祖先留下来的智慧，是教给我们礼貌、文明和理解，是张开双手拥抱其他的兄弟，是带着欣赏地目光与其他人交流。不是用这样地高姿态去评价他人的文明和文化。
我想未曾先生设立书格网站，也是抱着“求大同”的初衷，而不是为了这样用讥诮的语气评价其他的文化。
@正音悉达 #17170
你说“这句话当然要先问是不是，再去评价。”
那么请问“远在公元前约三千年的古巴比伦人就知道和应用勾股定理，他们还知道许多勾股数组。美国哥伦比亚大学图书馆内收藏着一块编号为“普林顿322”的古巴比伦泥板，上面就记载了很多勾股数。”
------古巴比伦早就灭国，没有语言和书籍传下来，怎么知道他们知道勾股定理？古巴比伦泥板是没有烧制的土坯，埋在地下5000年为什么不发潮变酥？那上面的刻字非常清晰，是不是伪造新刻的啊？
请问古巴比伦泥板是不是伪造的？如果是伪造的，那么古巴比伦是不是不知道勾股定理？
如果古巴比伦泥板不是伪造的，那么在客观上是不是很容易伪造呢，怎么区分和防止呢？
@gsyrzjy #17184
就事论事是一个好习惯 没必要每次都要把一个问题的回答衍伸到一个更宏大的问题之中
最开始我说你这么评价一本国外的旧书 语气和用词不当 你反问国外的数理研究与我国比之如何
我回答你文化之前平视 如实、中立地评价即可 这样带感情色彩不妥 你反问巴比伦文化是否真实存在
就事论事真的这么难吗？
（我可以提前告诉你：你所谓的多方面枚举，每一方面都是靠不住和伪造的！当然先从勾股定理开始，希望你不要逃避每一个问题！）
@正音悉达 #17186
因为你说了 “这句话当然要先问是不是，再去评价。”，这是一个为人的方法和态度问题，方法和态度本来就是一个宏大的圣母，它不仅只是用于别人的一件事，也用于你方的一件事！
我现在就用你方的一件事，来检验你说的方法和态度，是不是真的，是不是双标！！！
回到勾股定理和古巴比伦泥板，这可是一个小问题，一点也不宏大！我并不是只会宏大的问题，不会很小的问题，希望你也不是！！！！！
@gsyrzjy #17189
你要是一开始就亮出观点 说写了勾股定理的巴比伦泥板是伪造的 我才不跟你这浪费时间
@正音悉达 #17190
就在这里跳吧，别说废话！
@正音悉达 #17170
俗话说，灯不拨不亮，理不辩不明！有些事不得不说，有些理不得不辩。
不过，开始之前，我不得不先扶你一把，帮你纠正一下你的站姿：
“这是面对其他的文化如何自处的问题。”
这是你的原话，我给你加了一个句号。你的这个姿势比较陈旧了，估摸着已经保持了两三百年了吧，今天纠正你一下：
“这是一个其它国家面对中华文明该如何自处的问题。”
现在我们可以接着讨论了。
首先，你在上面回帖中说：
“计算之书是以歌谣形式记载这些东西的 有些就是为了押韵 再说文化不同 ……”
请你正面回答一下，此书是歌谣形式记载的吗？押韵吗？哪一个版本是歌谣体式？哪一段是在照顾押韵？是拉丁文原版，英文版？德文版？或者是中文版？如果不是，你这个命题如何而来？我上面罗列了证据，供参考！
其次，你在@gsyrzjy #17163的回帖中说：
“当然，经过多方面枚举后，往往却是得出来的结果是，中国古代数学理论上的建树不如国外。”
这句话其中有两个问题。其一，什么是你所说的“数学理论”？是公理定义证明吗？如果是，那为什么一定要有这套公理定义证明体系呢？如果能够很好地解决现实生活劳作中的数学问题的话，为什么一定要去证明和定义呢？不是脱裤子放那啥，多此一举吗？为什么？你想过没有？给你一点提示，学习别人的东西的时候，为了要弄明白别人的东西来龙去脉的时候，用的正是这套逻辑。其次，你说“经过多方面枚举后……中国建树不如国外。”请教你是怎么枚举的？枚举样本是哪些？如果枚举不出，请你不要像上面“计算之书是以歌谣形式记载这些东西的 有些就是为了押韵”这样信口开河，现在的中国人不好骗了！为了表达我的疑问，我来先帮你枚举一些：
位值制十进位记数法；加减乘除四则运算，开方，开立方；勾股定理；勾股（割圆术，三角）；算表（大九九，小九九）；分数运算；十进位小数；正负数；算术应用——九章中早有各种类型的应用问题；联立一次方程组；二次方程；三次方程；高次方程——其中王文素解高次方程的方法，较英国的霍纳 (Hirner，1786－1837)、意大利的鲁非尼 (Ruffini，l765－1822) 早近 300 年；在解代数方程上，他走在 17 世纪牛顿 (I．Newton，1642—1727)、拉夫森 (J． Raphson，1648－1715) 的前面 140 多年，率先用导数逐步迭代求解；联立高次方程组与消元法；各种辅助算具——筹算（一数一筹，九数一筹，有横竖两种），笔算，算盘；圆周率；密率；极限；级数——缀术；插值法——我国古代数学中的招差术……
你倒是能够枚举一下，“其它文化”的数学落后于中国有哪些，这样比较合适一点。
你又说：
“但是我想反问，凭什么中国古代所有的方面，都要领先于其他国家？……”
我从来没说过这个话哦，是你自己说的。不要假装看不见我提供的证据，顾左右而言其它哦？！是你在扩大讨论的范围哦，不是别人！
最后，你说：
“但是祖先留下来的智慧，是教给我们礼貌、文明和理解，是张开双手拥抱其他的兄弟，是带着欣赏地目光与其他人交流。不是用这样地高姿态去评价他人的文明和文化。”
我们就事论事，一码归一码。怎么，我们只是想要搞清楚别人告诉我们的话是真还是假的时候就说我们“不礼貌”“高姿态”，别人在我们地头上胡说八道，瞎编乱造的时候你就能视而不见？——这是赤裸裸的双标，和那个什么哔哔西之流一样的套路！
我们只是正本清源，好让我们的子孙后代看清楚自己文明的真面目，以后不要像你一样跪着，这姿势不好看！所以，我们的归我们，他们的归他们，明白了吗？
事实胜于诡辩，而诡辩成就不了文明的伟大！
中国农村俗语：子不嫌母丑，狗不嫌家贫！一个连自己的过去都不敢正视，都要靠谎言来编造历史，构建自己内心脆弱的尊严，从而凌驾于世界其它文明之上的“文明”是没有前途的！
@gsyrzjy #17192
其实，我开头只是想找一个参照对象，好体现中国数学之美，根本没想和人辩伪，他自己蹦出来的，不管我们的事！另，多谢兄台。
又有，《孙子算经·卷下》一题：
题：“今有物，不知其数。三、三数之，剩二；五、五数之，剩三；七、七数之，剩二。问物几何？”
答：“答曰：二十三。”
术（算法，具体的解题步骤）：“术曰：‘三、三数之，剩二’，置一百四十；‘五、五数之，剩三’，置六十三；‘七、七数之，剩二’，置三十。并之，得二百三十三。以二百一十减之，即得。凡三、三数之，剩一，则置七十；五，五数之，剩一，则置二十一；七、七数之，剩一，则置十五。一百六以上，以一百五减之，即得。再看斐波那契《计算之书》(12 章)有一题：
“设计一个数，除以3，除以5，也除以7 ……对于除以3，所剩余的每个单位1，要记住70；对于除以 5，所剩余的每个单位 1，要记住 21；对于除以7所剩余的每个单位1，要记住 15。这样的数如大于 105，则减去105，其剩余就是所设计的数。”
就是不知道，那时候有没有学术舞弊一说？！比较上面两本书对同一题的描述，谁是原本，谁是抄袭，非得要我说的这么直白？
又有《九章算术·卷六》“均输章”第二十题，凫雁相逢 ：
题：“今有凫起南海，七日至北海；雁起北海，九日至南海。今凫雁俱起。问︰何日相逢？”
答：“答曰：三日、十六分日之十五。”
术：“术曰：并日数为法，日数相乘为实，实如法得一日。”
试以西式数学方法解释此术。①并日数为法 → 7+9=16（法）；②日数相乘为实 → 7×9=63 ；③实如法得一日 → 16×t=63 → t=63/16，即3又15/16。
再看《计算之书》第12 章，两船相遇：
“两只船相距一定的距离，第一只船需要 5 天才可以驶完这段路程，另外一只需要 7 天。如果同时出发它们需要多少天才会相遇？你把 5 乘以7，得到 35，假设它们用了35 天相遇，在这些天中第一只船行进了 7 倍的旅程，另外一只船行进了 5 倍的旅程，因此你把 5 加上 7，得到 12，因此这是两只船之间的旅程的 12 倍。你把1 乘以 35，除以12，得到的商是 2又11/12（分数哦！）， 因此在这些天数里它们相遇了。如果你希望知道它们在哪里相遇，则你把 7 和5 除以 12，因此结果是第一只船行进了整个旅程的7/12第二只行进了 5/12。如果第一只船在一天中向着第二只船的方向行进了 1/7，第二只在一天中前进了 1/5，你把 1 除以 12，商就是它们相遇的时间，相遇的地方就是上述的地方。”
所以外国很早就出版了“译著”。最早的学术腐败。
@生 #17207
西方要是说清楚这是翻译本，底本来自中国古代算书，是吧，没人指责他们，然而你却非要说是自己写的，那问题就严重了，说好听点叫抄袭，说不好听那就是剽窃。是不是？说是“学术腐败”那还是轻的，没有触碰到问题的实质。
中国人实诚，在古代估计从来没有“知识产权”这个概念，即使是今天，很多民间手艺人依旧没有这些概念，只要外国人来学，都是倾囊相授。然而人心隔肚皮啊，人家转身就注册，回头就问你收版权费！
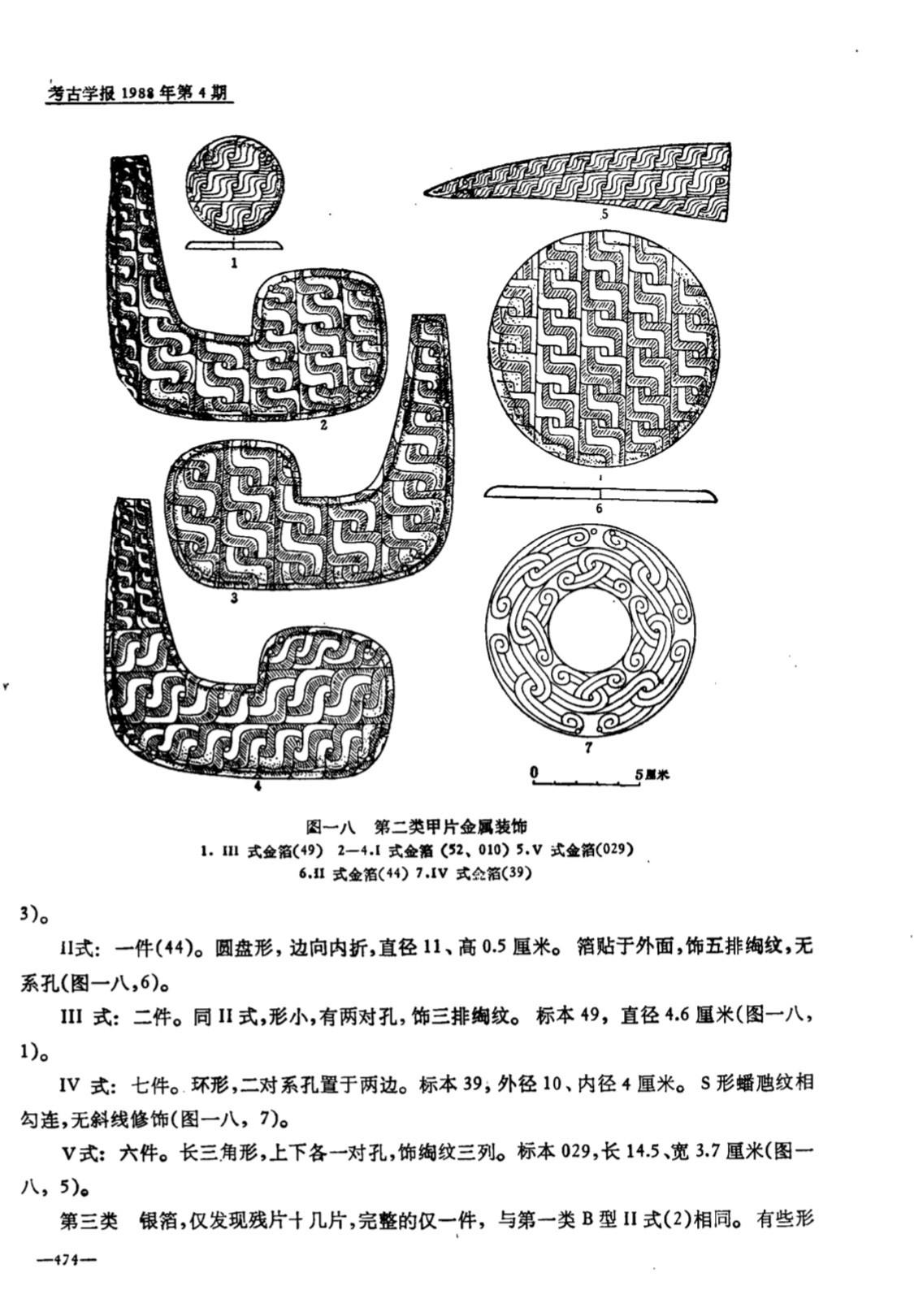
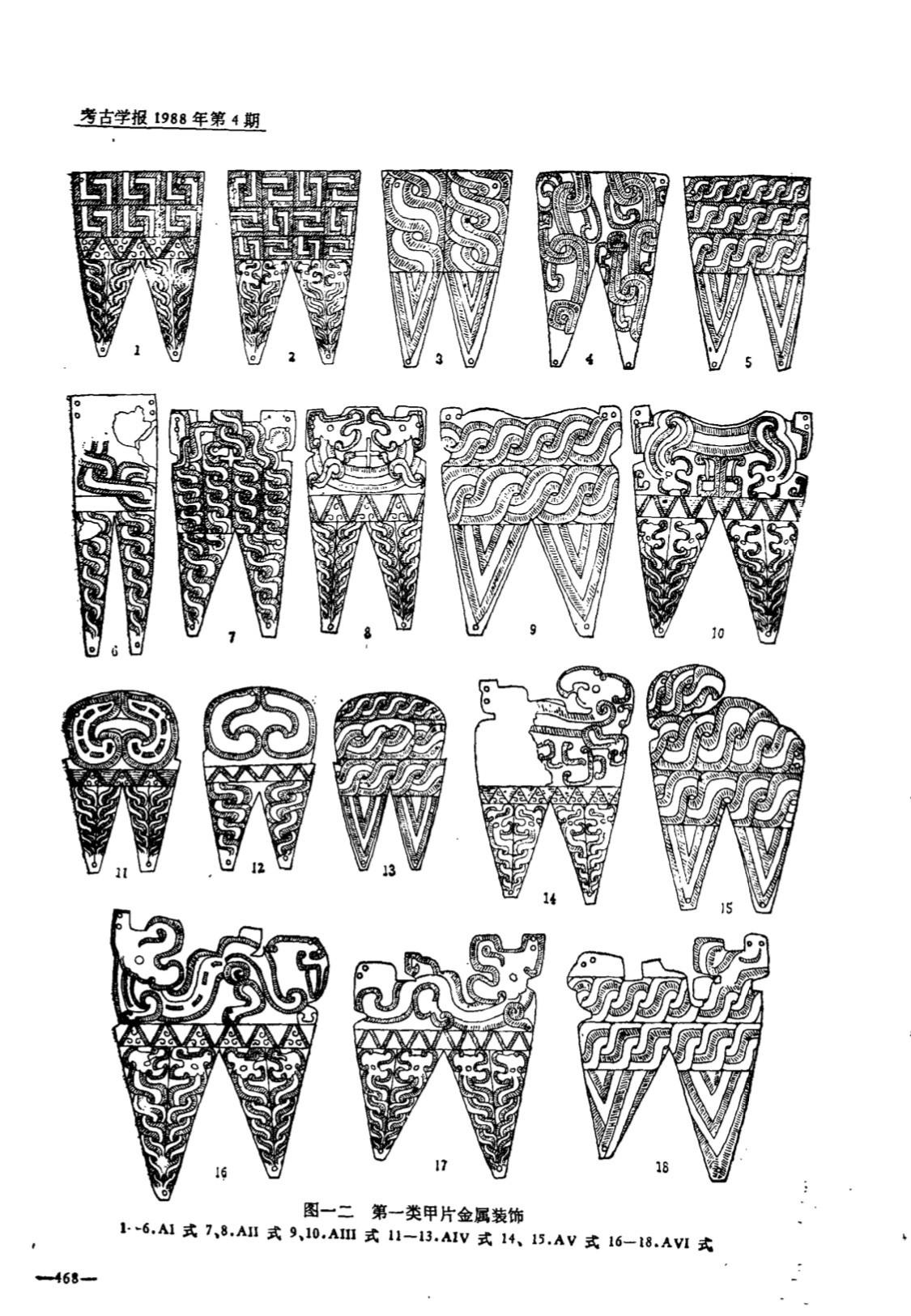
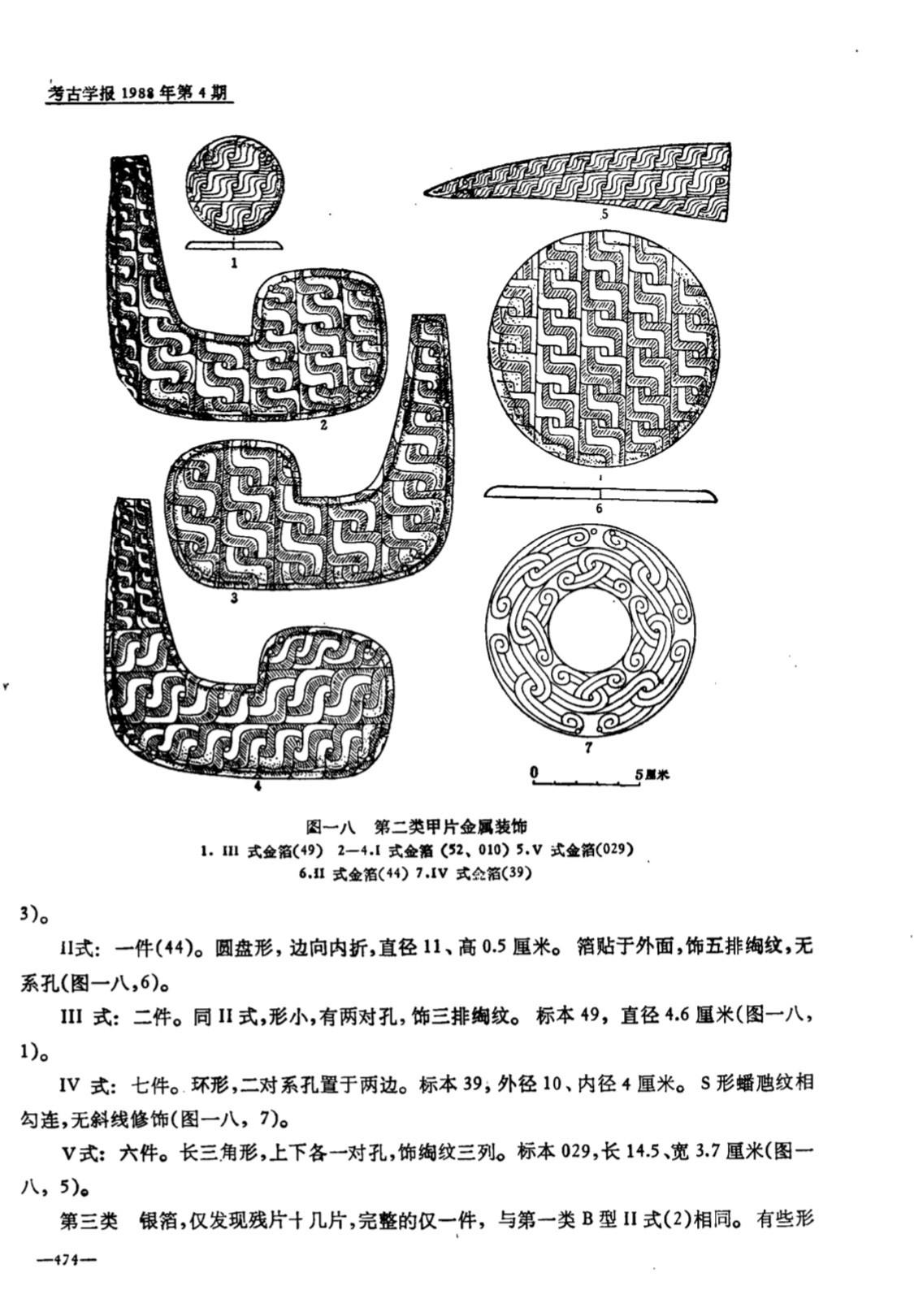
甲片金属装饰 ——春秋晚期，宜昌当阳曹家岗5号楚墓出土
这不是数学，不是几何？有一位朋友说的好：“甲片真好看，这么一身黄金甲，如果再相貌堂堂一些，宛如天～神～”《九章算术·卷八》“方程”第十题，关于甲乙持钱的问题：
题：“今有甲乙二人持钱不知其数。甲得乙半而钱五十，乙得甲太半三分之二，见《夏侯阳算经·卷上·明乘除法》而亦钱五十。问：甲、乙持钱各几何？”
答：“答曰：甲持三十七钱半，乙持二十五钱。”
术：“术曰：如方程，损益之。” 法曰《九章详注比类演算法大全》：“甲欲乙中半，乙母二分子之一；乙欲甲之太半，甲母是三分子之乃之二。以甲母三分乘乙钱五十，得一百五十，复以乙母二分乘甲钱五十得一百。以少减多，乙钱余五十，半之得乙钱二十五。复以乙钱二十五，甲钱一百，以少减多，甲钱余七十五，半之得甲钱三十七文半。”
用现在西方表达方式计算大致如此：
再看《计算之书》第 12 章有一题 ：
“两个人有一些便士， 一个对另外一个说 ，如果你给我一个便士， 则我的就和你一样 。另外一个回答 ，如果你给我一个你的便士， 则我将有你十倍的便士。”
@九靈 #17199
别客气
“这句话当然要先问是不是，再去评价。”
“就事论事真的这么难吗？”
“我才不跟你这浪费时间”
------一会儿就有双标、三标、四标了，对方可真是方法论大师！
结论：
第一个方面勾股定理的西方优势，对方避而不答，说明没有优势可答！
那么对方所谓的“多方面枚举（的西方优势）”，不过是谎言！
@gsyrzjy #17223
他能枚举个啥？！西方在16世纪末17世纪初耶稣会士来中国明朝之前能有啥？都到17世纪初了，连算个乘除，开方开立方都嫌难的地方能有个啥数学？
@九靈 #17221
事实上，本题的算法“术曰：如方程，损益之。” 中说的“损益之”就是现在所谓的“高斯消元法”。我们高数学习的高斯消元法其实就是中国解线性方程组的古法，在《九章算术》公元一世纪左右？中早已成型，一直沿用至今，有两千多年历史了吧，远远早于德国高斯的“发明”，高斯生于1777年，所以，问题是，真的是高斯想出来的“高斯消元法”吗？
《九章算术》成书的年代中国还没有被西方“污染”，没有所谓的“西算”的x，y。解题的步骤是先列出方程，就是列出今天线代的线性方程组的增广矩阵，然后用方程术求解。方程术对列出的方程即增广矩阵进行“偏乘”与“直除”两种变换，将矩阵化为阶梯形矩阵，其实就是今天初等变换中的“倍法变换”和“消法变换”。
我再用九章算术古法解一遍这道题。先布筹，我这里用数字替代，在布题板上列出增广矩阵，中国古代古书是直写的，竖排称为行，因此列方程如下：
1 2/3 2 2 2 0 2 0
1/2 1 ———> 1 3 ———> 1 -2 ———> 1 1
50 50 100 150 100 -50 100 25
2 0 1 0
———> 0 1 ———> 0 1
75 25 75/2 25
这样就获得了我们想要的答案。这种方法我们现在的高数教科书中都叫“高斯消元法”，其实就是我们古代的“方程术”。
@九靈 #17225
哈哈
@九靈
刚看到一个有意思的文章：中国古代也有微积分：
九章算术：术曰：半周半径相乘得积步。
S=1/2 L . 1/2 D=1/2 （2πr） . 1/2 （2r）=πr²
先有公式后有刘徽证明，如果古人不懂微积分，怎么能先得出公式呢？
详见文章https://baijiahao.baidu.com/s?id=1599852997894476511&wfr=spider&for=pc
（文中的圆面积公式有误，已重推如上，但不影响结论）
估计是汉武帝罢黜百家，不能当官，让许多东西失传了，因为学了没用
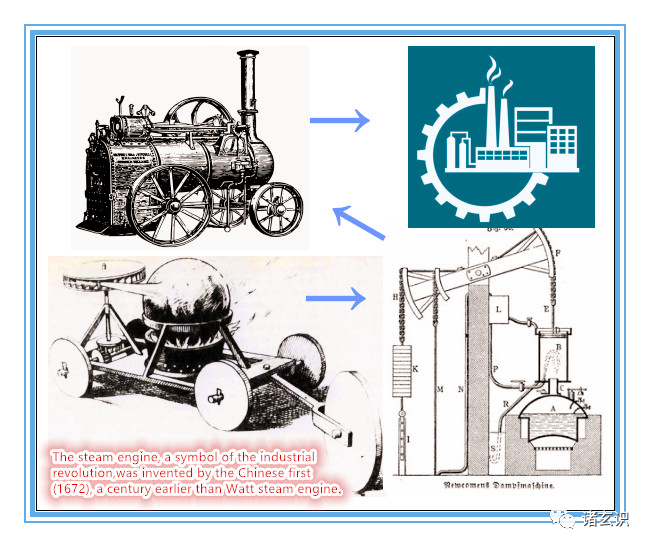
西方的贡献真正的是蒸汽机，因为在蒸汽机以前，任何的知识、技术都是负担、都是奇技淫巧、都必须在父母的棍棒下消灭
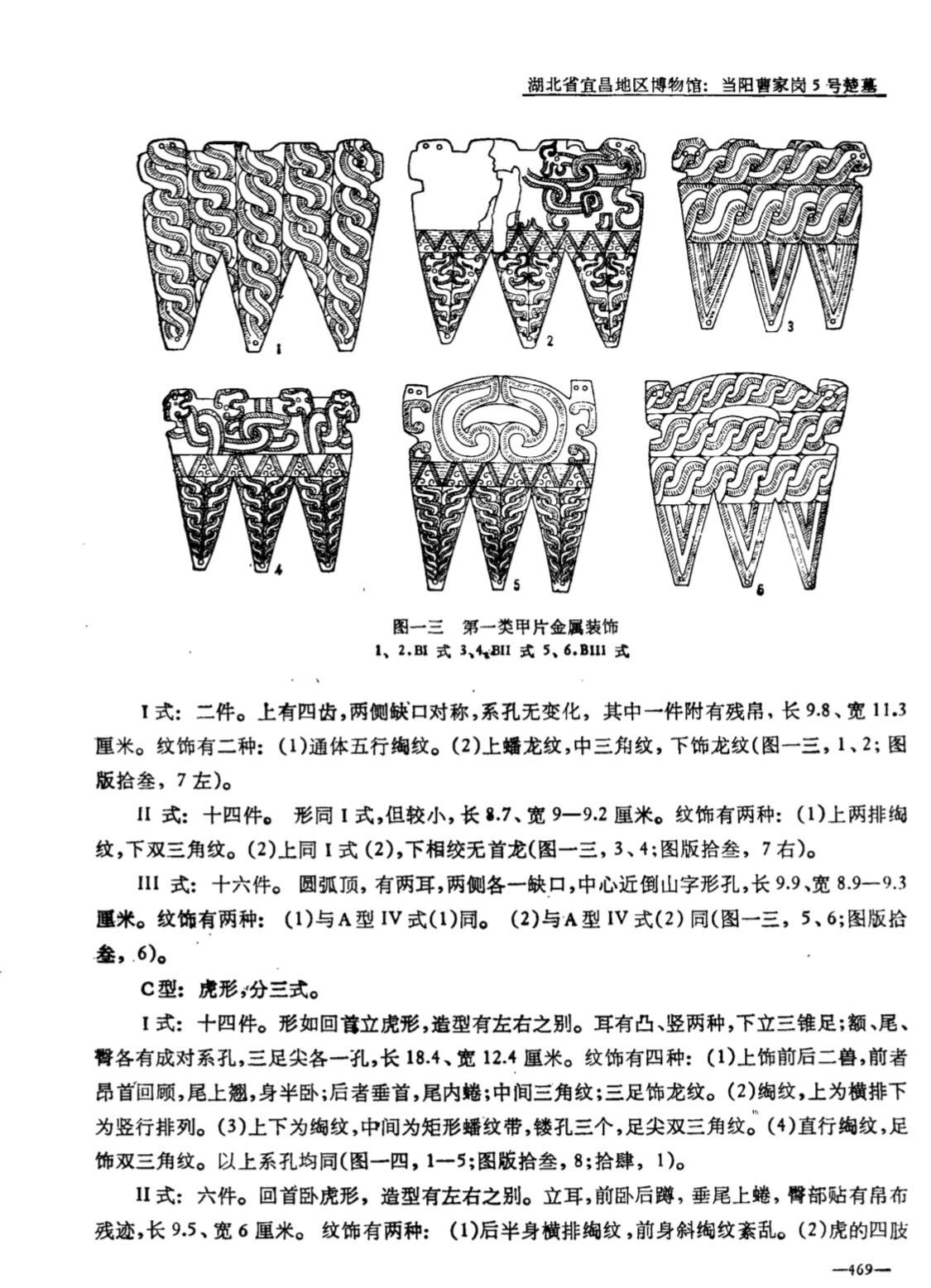
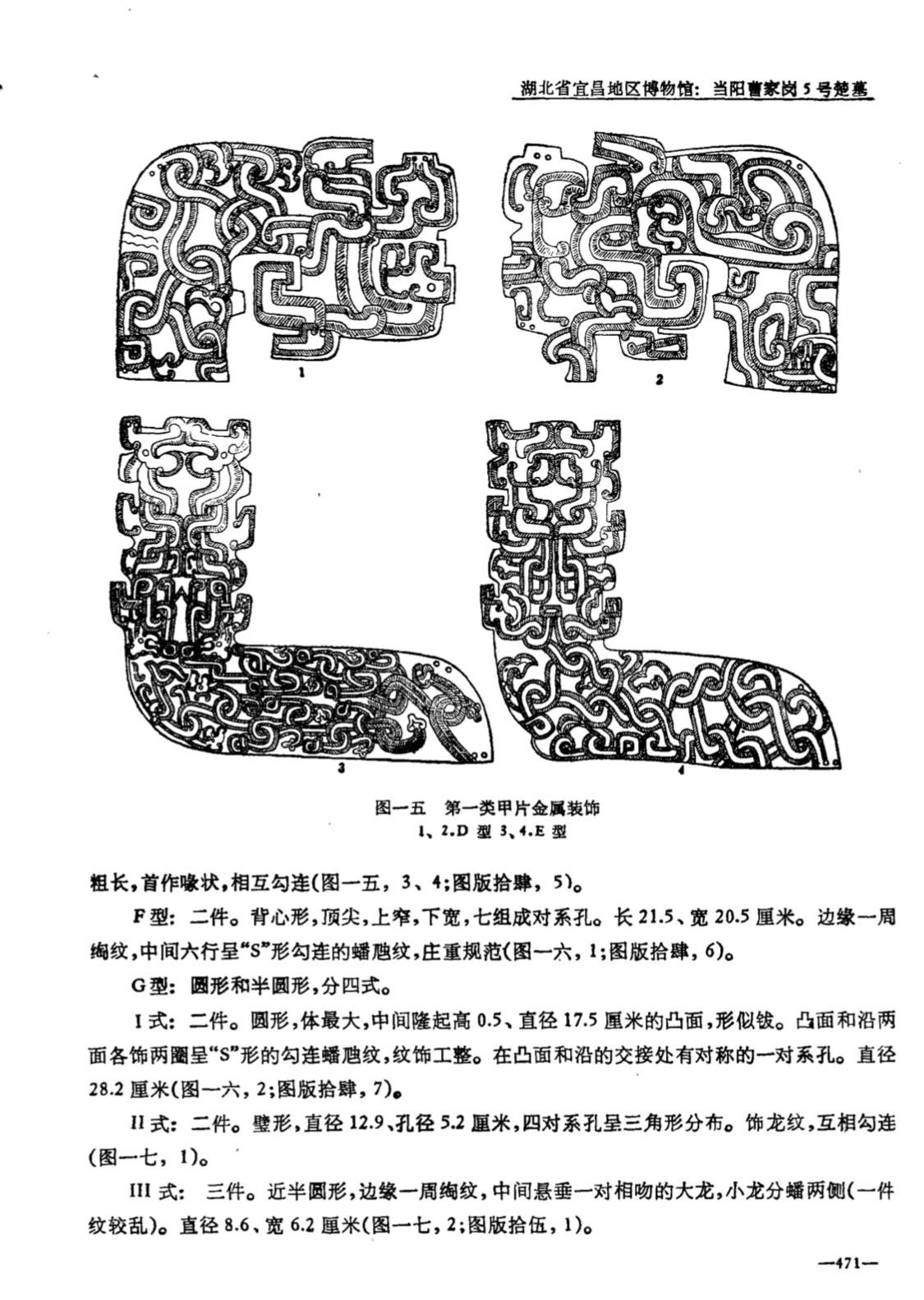
甲片金属装饰 ——春秋晚期 宜昌当阳曹家岗5号楚墓出土
妥妥的数学，妥妥的几何学知识！实用器哦，中国古代没有玄之又玄的古希腊不食人间烟火的高大上的公理证明哦！有一位朋友说的最直接：“甲片真好看，这么一身黄金甲，如果再相貌堂堂一些，宛如天神。”不是吗？果然不是什么好东西！一样的“冷冷”的声音，一样的放冷箭，一样的无下文，一样的高姿态，一样的腹中空空，一样的“狄克”，吐
不过是一只政委
@gsyrzjy #17243
作为工业革命标志的蒸汽机，是中国人最早发明的（1672年，图中左下方的机器——蒸汽四轮汽车），比瓦特蒸汽机早一个世纪。耶稣会士南怀仁加入了中国工程师团队的研制，他把相关信息带到了欧洲。
又有《九章算术·卷六》“均输章” 有一题：
题：“今有善行者行一百步，不善行者行六十步。今不善行者先行一百步，善行者追之。问几何步及之？”
答：“答曰：二百五十步。”
术：“术曰：置善行者一百步，减不善行者六十步，余四十步，以为法。以善行者之一百步乘不善行者先行一百步，为实。实如法得一步。”
按：“按：此术以六十步减一百步，余四十步，即不善行者先行率也；善行者行 一百步，追及率。约之，追及率得五，先行率得二。于今有术，不善行者先行一 百步为所有数，五为所求率，二为所有率，而今有之，得追及步也。”
又接上题继续问：
题：“今有不善行者先行一十里，善行者追之一百里，先至不善行者二十里。问善行者几何里及之？”
答：“答曰：三十三里少半里。”
术：“术曰：置不善行者先行一十里，以善行者先至二十里增之，以为法。以不善行者先行一十里乘善行者一百里，为实。实如法得一里。”
按：“按：此术不善行者既先行一十里，后不及二十里，并之，得三十里也，谓之先行率。善行者一百里为追及率。约之，先行率得三，三为所有率，而今有之， 即得也。其意如上术也。”
又一题：兔走犬追
题：“今有兔先走一百步，犬追之二百五十步，不及三十步而止。问犬不止，复行几何步及之？”
答：“答曰：一百七步七分步之一。”
术：“术曰：置兔先走一百步，以犬走不及三十步减之，余为法。以不及三十步乘犬追步数为实。实如法得一步。”
按：“按：此术以不及三十步减先走一百步，余七十步，为兔先走率。犬行二百 五十步为追及率。约之，先走率得七，追及率得二十五。于今有术，不及三十步为所有数，二十五为所求率，七为所有率，而今有之，即得也。”
再看人家斐波那契《计算之书》第 12 章的“狐走犬追”题🤔🤔🤔：
“有一只逃跑的狐狸它在一只狗前面 50 步远的地方，狐狸每前进 6 步狗就跟随它前进 9 步。事实上这个问题可以利用鸡蛋问题的规则来计算，也就是你把9 减去 6，剩下 3，你把 50 乘以 6 除以 3 ，得到的商是100 步，也就是狐狸跑了这些距离使得狗与它到了同样的地方。事实上如果你忽略了他们的距离，假设在狐狸前进了 100 步之后狗赶上了它，你把 100 乘以 3，除以前面所说的 6。”
春秋战国秦汉错金银工艺中的数学。
台北故宫收藏的汉代错金云纹卮
金银错青铜器多用几何纹装饰，其中尤其以几何云纹最多见。
金银错几何云纹，与以往青铜器的几何云纹不同，其主要特点是，它既有几何图案所固有的严谨规则构成的骨法，而又在规则中求变化。如多使用细而匀称的云纹涡线，而旋转的细涡线之间，是用较宽的面来联结，这种纹饰富有节奏感和律动美，显得格外清新和活泼。几何图案的创新，是战国秦汉金银错工艺一个突出的艺术成就。此外，几何图案，还有菱纹、三角纹、雷纹、勾连纹等，但都不是主要纹饰。看看这几个战国几何纹铜壶，至少也是2242年前的老物件了，其中的数学几何美术以及工艺，都达到了顶尖的水平。
@九靈 #17320
这完了，我又中毒了，蒸汽机原来也是中国的
约1679年法国物理学家丹尼斯·帕潘在观察蒸汽逃离他的高压锅后制造了第一台蒸汽机的工作模型。同时代的萨缪尔·莫兰也提出了蒸汽机的主意。
------------1679年确实晚于1672年，这这
@九靈 #17324
朋友资料好丰富啊，研究也挺深的挺广的，最重要的是有理有据。
我来，我来说说公知们（此处的公知特指双标的，是贬义，并非“公共知识分子”的原意）的话，让他们无话可说——
1，中国古代数学那么牛，怎么近现代以来这么落后？（对中西方古代历史都一知半解的）
2，你们说的中国古代数学这么流弊，那么诺贝尔数学奖怎么没见一个中国籍的人（华人当然不算啦，肯定要说中国精英都喜欢往外跑啦）？（对近现代西方科学和近现代中国史都一知半解的）
3，祖宗这么厉害，然鹅我们现在什么都不是，处处都是抄国外的，真的说明了“崖山之后无中国”“华夏正统在扶桑”，所以人家日本人获得诺贝尔奖不断，对吧？（对日本史也不了解的）
4，你们说西方的著作是伪书，呵呵，民国大师们早就说过了，中国的书有多少是伪造的、胡说八道的？好像《尚书》就是伪书呢！再说中西方古代交流也不少，焉知中国古代数学著作不是抄袭人家国外的，只不过人家没有留下来罢了！（一知半解的文科生最喜欢类似的话术）
5，都说数学和逻辑相关，也和哲学相关，那么中国古代怎么就没有像人家康德、笛卡尔、牛顿这样的哲学家呢？啥，牛顿是哲学家，你不知道吧，果然中国的教科书都是骗人的、洗脑的……中国全面落后，就从不正视自己开始的！哲学，是科学之母，没有西方哲学，就没有一切现代科技和文明！归根到底还是人家希腊自古就有皿煮的政治理念和自由的学术氛围……（还知道一点西方史却不知道中国史的文科生，一张口百分百各种“主义”，从实用到存在的那种，归根到底就是皿煮和自由，最后说不定还来一句神学早已在山巅等待科学了。）
6，嗯……想好了再编吧……（日本外务省和美国民主基金会的钱这个月没到账啊！跪爸爸是真，恨自己一身黄皮肤也是真，爸爸怎么不给钱呢，真是的。）
【还用加狗头么？欢迎补充、抬杠、反怼……】
@gsyrzjy #17326
“法国物理学家丹尼斯·帕潘在观察蒸汽逃离他的高压锅后……”
我在西方十几年，观察他们的饮食方式以前从来没有用蒸汽煮食的习惯，用蒸汽蒸食物还是近年来的偶尔使用的方法，这样归功于电器商了。想想17世纪他们怎么会忽然观察蒸汽的了呢？甚至用上了高压锅？发明高压锅来干什么？反正肉都是烤的，用高压锅蒸土豆吗？说到这里高压锅的发明又是一个大问题了，到底是谁发明了高压锅？这个留待以后再讨论。一个连煮食和蒸食食物的烹饪习惯都没有的地方，能观察蒸汽？能想到造高压锅？
反观中国，最晚至先秦时期就已经开始使用蒸汽做饭了，比如中国先秦时期的蒸食用具甗，可分为两部分，下半部是鬲（锅），用于煮水，上半部是甑，用来放置食物，可通蒸汽。
可见，只有中国（包括其它中国文化圈的国家）才最有可能发现蒸汽的奥秘。从而进一步发展到对蒸汽的运用。这是顺理成章的，非常符合常理，符合逻辑的事情。
@旭公子 #17327
都是网友的功劳，我不过是搬运一下而已 😅！
@书生 #17331
他们的话术有一个鲜明的特征，没有真凭实据，张口就来！反正你反驳他们就要去花时间找各种证据以及逻辑漏洞，所以说，造谣一张嘴，辟谣跑断腿。一般人还真没这份精力和时间耗在这个上面，所以网络上才能铺天盖地都是玄幻小说一样吹嘘西方的网文！指鹿为马，颠倒黑白，抹黑造谣都是他们最基本的本事。然而他们不懂一个最基本的道理，假的永远是假的，真的永远是真的。假的成不了真，而真的也不会变成假，几十年，几百年你可以骗，那么千年后呢？真相犹如堆积在灰烬下面隐隐燃烧的烘烘的炭火，等表面的灰烬被风一吹，炭火就会显露出它灼人的热力来！
@书生 #17331
哈哈
@九靈 #17345
说得好！！！！
哦，这是甑，开了眼界
- 话题“中国古代数学书多美啊！”已关闭，不接受新回复。
